中心極限定理

大数の法則と中心極限定理

大数の法則・中心極限定理をわかりやすく掘り下げて説明します.

大数の法則

大数の法則
ある試行を膨大に繰り返すと平均(標本平均)は真の平均にめっちゃ近づくよ
ただし,ある試行の分布は互いに独立であり,平均・分散が存在することが条件だよ

実際にその様子を見てみましょう.
偏りのないサイコロを何回もふることにします.大数の法則によれば,非常にたくさん繰り返せば,ほぼ真の平均(1/6≒16.7%)になるということです.

100回ふってみた

まだバラバラだ,均等になるのかなぁ

1000回ふってみた

3の回数が少ないなぁ

100000回ふってみた

おぉ,ほぼ均等になっている!

1000回では3の出た回数が少ないですが,100000回繰り返すと,全て均等になっています.
「1000回で3の出た回数だけが少ないぞ.でも最終的には全部ほぼ同じ回数になるんだから,これからは3が多く出るっしょ！」
と思うかもしれませんが,それは間違いです.
正しい解釈としては,
3の出た回数が少ないから、多く出はじめることによって一定値に収束していくのでなく、試行回数が多くなる事で、それぐらいの差は誤差になっていくため、確率的に収束していく
ということです.
しかも,サイコロ を投げるという試行は独立であるということからも,突然ある目が出やすくなるなんてことはあり得ませんね.

中心極限定理(CLT)

大数の法則によって,最終的に真の平均に近くなることはわかりました.では実標本平均と真の平均とのズレはどれくらいなのかということについて議論しているのが中心極限定理(CLT)です

中心極限定理(CLT)
標本平均と真の平均との差の分布は正規分布に収束するよ
ただし,標本は互いに独立であり,平均・分散が存在することが条件だよ

試行回数を非常に多く繰り返せば,実際に得られた平均と真の平均とのズレは正規分布になるということです.

中心極限定理を少し言い換えると以下のようになります

中心極限定理(CLT)
ある分布に従う多数の変数の和の分布は正規分布に収束するよ
ただし,変数の分布は互いに独立であり,平均・分散が存在することが条件だよ

つまり,異なる分布から得られる値を合わせると最終的に正規分布に収束するという定理です.
下の図では,標本数を変化させて指数分布に従う値の和の推移を表しています.正規分布に近づいていることがわかります.

指数分布に従う値の和の分布の変化

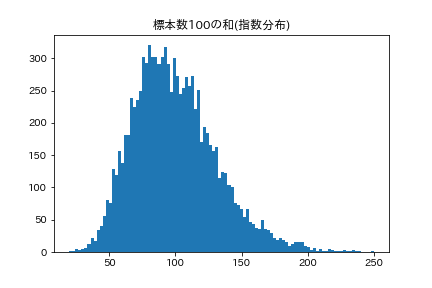
ここで勘違いしがちなのですが,全ての分布が正規分布に近似されるわけではありません!
大数の法則・中心極限定理をもう一度見てみてください.
「分布は互いに独立であり,平均・分散が存在することが条件」と書いてあります.
つまり,平均または分散が存在しない分布は大数の法則・中心極限定理が成り立ちません.
例としては,コーシー分布は平均が存在しないため,大数の法則や中心極限定理が成り立ちません.
もちろん独立でない試行(時系列など)では大数の法則や中心極限定理が成り立ちません.